3/14/15 a las 9:26:53: hoy es el día de Pi más preciso que vivirás
El Pi Day es una tradición que se celebra en varios lugares del mundo, especialmente en facultades y escuelas de matemáticas, el 14 de Marzo (3/14 en formato americano). El de esta ocasión será único será único porque coincide el año (15) y los dígitos de la hora (92653).
π=3,1415926536
La primera constancia que se tiene del singular evento es de hace 26 años en el San Francisco Exploratorium. Desde entonces se viene celebrando con relativa constancia y ha ido ganando poco a poco en popularidad. Google le dedicó un doodle en 2010 y la cámara de los representantes estadounidense lo reconoce oficialmente.
El momento exacto será a las 9 horas, 26 minutos y 54 segundos (redondeado), instante en el que, usando el formato americano donde el mes va antes que el día, la fecha y la hora coincidirán número por número con los 10 primeros dígitos del número pi.
Si alguno quiere ser un poco más preciso, alguien se ha tomado la molestia de calcular el momento a nivel infinitesimal. Será, exactamente, a las 9:26:53.58979, un instante antes de que la aguja marque los 54 segundos.
No ocurrirá de nuevo hasta dentro de 100 años, en el 2115, así que hay bastantes posibilidades de que para la próxima no estemos aquí para contarlo.
Imagen: tschitscherin/Shutterstock
FUENTE: http://es.gizmodo.com/3-14-15-a-las-9-26-53-hoy-es-el-dia-de-pi-mas-preciso-1691280280
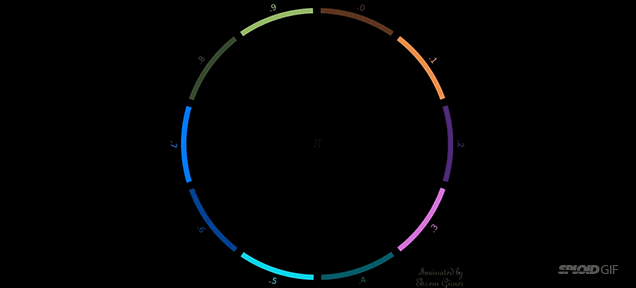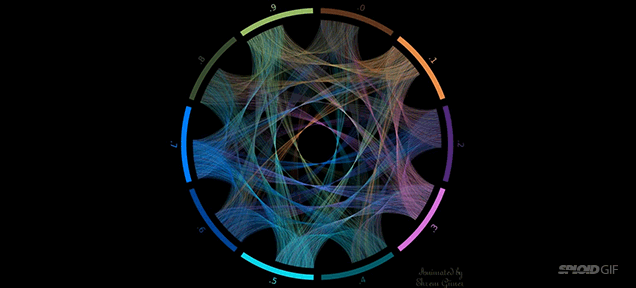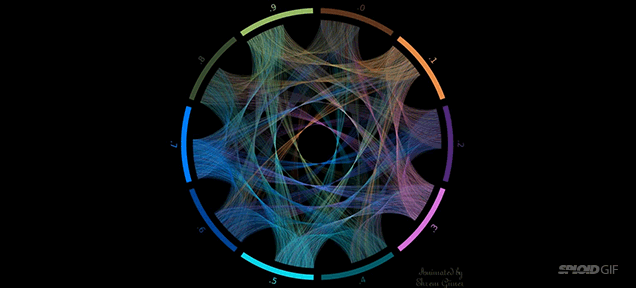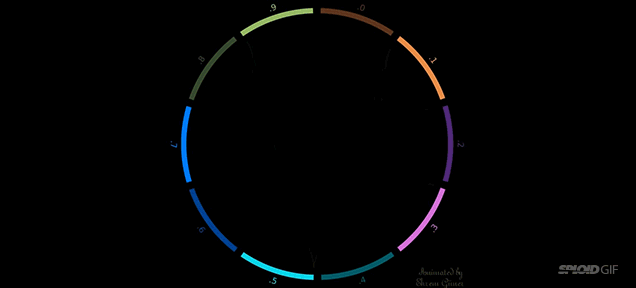
Cristian Ilies Vasile ha credo la visualización más bonita que he visto del número Pi. Primero dividió un círculo en 10 segmentos, del 0 al 9. Luego trazó una línea desde el tercer segmento al primero. Del primero, la línea salta al 4, luego al 1, luego al 5, y así sucesivamente. Es la representación de Pi como transiciones de líneas entre sus dígitos. La ilustración final es brillante y preciosa.
FUENTE: http://es.gizmodo.com/esta-es-probablemente-la-representacion-mas-bonita-del-1566984184
FUENTE: http://es.gizmodo.com/esta-es-probablemente-la-representacion-mas-bonita-del-1566984184
VIDEO DE LA IMAGEN: https://www.youtube.com/watch?v=uKuG4qqtP1Q
FUENTE:
http://es.gizmodo.com/esta-es-probablemente-la-representacion-mas-bonita-del-1566984184
EL NÚMERO PI
π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Cabe destacar que el cociente entre la longitud de cualquier circunferencia y la de su diámetro no es constante en geometrías no euclídeas.
FUENTE: http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80
El nombre π[editar]
La notación con la letra griega π proviene de la inicial de las palabras de origen griego περιφέρεια 'periferia' y περίμετρον 'perímetro' de un círculo,1 notación que fue utilizada primero por William Oughtred (1574-1660) y cuyo uso fue propuesto por el matemático galésWilliam Jones2 (1675-1749); aunque fue el matemático Leonhard Euler, con su obra Introducción al cálculo infinitesimal, de 1748, quien la popularizó. Fue conocida anteriormente como constante de Ludolph (en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (que no se debe confundir con el número de Arquímedes). Jones plantea el nombre y símbolo de este número, en 1706 y Euler empieza a difundirlo, en 1736.3
Se le conoce también con el nombre de Constante de Arquímedes, quien lo calculó con la aproximación de  < π <
< π <  , tal como consignó en su obra "Medición del círculo", ciertamente con otra notación.4
, tal como consignó en su obra "Medición del círculo", ciertamente con otra notación.4
 < π <
< π <  , tal como consignó en su obra "Medición del círculo", ciertamente con otra notación.4
, tal como consignó en su obra "Medición del círculo", ciertamente con otra notación.4
FUENTE: http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80
Historia del cálculo del valor π[editar]
La búsqueda del mayor número de decimales del número π ha supuesto un esfuerzo constante de numerosos científicos a lo largo de la historia. Algunas aproximaciones históricas de π son las siguientes.
Antiguo Egipto[editar]
El valor aproximado de π en las antiguas culturas se remonta a la época del escriba egipcio Ahmes en el año 1800 a. C., descrito en elpapiro Rhind,5 donde se emplea un valor aproximado de π afirmando que el área de un círculo es similar a la de un cuadrado cuyo lado es igual al diámetro del círculo disminuido en 1/9; es decir, igual a 8/9 del diámetro. En notación moderna:
Entre los ocho documentos matemáticos hallados de la antigua cultura egipcia, en dos se habla de círculos. Uno es el papiro Rhind y el otro es el papiro de Moscú. Sólo en el primero se habla del valor aproximado del número π. El investigador Otto Neugebauer, en un anexo de su libro The Exact Sciences in Antiquity,6 describe un método inspirado en los problemas del papiro de Ahmes para averiguar el valor de π, mediante la aproximación del área de un cuadrado de lado 8, a la de un círculo de diámetro 8.
Mesopotamia[editar]
Algunos matemáticos mesopotámicos empleaban, en el cálculo de segmentos, valores de  igual a 3, alcanzando en algunos casos valores más aproximados, como el de:
igual a 3, alcanzando en algunos casos valores más aproximados, como el de:
 igual a 3, alcanzando en algunos casos valores más aproximados, como el de:
igual a 3, alcanzando en algunos casos valores más aproximados, como el de:Referencias bíblicas[editar]
Una de las referencias indirectas más antiguas del valor aproximado de π se puede encontrar en un versículo de la Biblia:
«Hizo fundir asimismo un mar de diez codos de un lado al otro, perfectamente redondo. Tenía cinco codos de altura y a su alrededor un cordón de treinta codos».I Reyes 7:23-24 (Reina-Valera 1995)
Una cita similar se puede encontrar en Segundo Libro de las Crónicas. En él aparece en una lista de requerimientos para la construcción del Gran Templo de Salomón, construido sobre el 950 a. C.:
«También hizo un mar de metal fundido, el cual tenía diez codos de un borde al otro, enteramente redondo; su altura era de cinco codos, y un cordón de treinta codos de largo lo ceñía alrededor».II Crónicas 4:2 (Reina-Valera 1995)
Ambas citas dan 3 como valor de π lo que supone una notable pérdida de precisión respecto de las anteriores estimaciones egipcia y mesopotámica.
Antigüedad clásica[editar]
El matemático griego Arquímedes (siglo III a. C.) fue capaz de determinar el valor de π entre el intervalo comprendido por 3 10/71, como valor mínimo, y 3 1/7, como valor máximo. Con esta aproximación de Arquímedes se obtiene un valor con un error que oscila entre 0,024% y 0,040% sobre el valor real. El método usado por Arquímedes7 era muy simple y consistía en circunscribir e inscribir polígonos regulares de n-lados en circunferencias y calcular el perímetro de dichos polígonos. Arquímedes empezó con hexágonos circunscritos e inscritos, y fue doblando el número de lados hasta llegar a polígonos de 96 lados.
Alrededor del año 20 d. C., el arquitecto e ingeniero romano Vitruvio calcula π como el valor fraccionario 25/8 midiendo la distancia recorrida en una revolución por una rueda de diámetro conocido.
Matemática china[editar]
El cálculo de pi fue una atracción para los matemáticos expertos de todas las culturas. Hacia 120, el astrónomo chino Zhang Heng (78-139) fue uno de los primeros en usar la aproximación  , que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.8 Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir9 que 3,14 era una buena aproximación, usando un polígono de 9610 o 1928 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.10 11
, que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.8 Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir9 que 3,14 era una buena aproximación, usando un polígono de 9610 o 1928 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.10 11
 , que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.8 Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir9 que 3,14 era una buena aproximación, usando un polígono de 9610 o 1928 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.10 11
, que dedujo de la razón entre el volumen de un cubo y la respectiva esfera inscrita. Un siglo después, el astrónomo Wang Fang lo estimó en 142/45 (3,155555), aunque se desconoce el método empleado.8 Pocos años después, hacia 263, el matemático Liu Hui fue el primero en sugerir9 que 3,14 era una buena aproximación, usando un polígono de 9610 o 1928 lados. Posteriormente estimó π como 3,14159 empleando un polígono de 3.072 lados.10 11
A finales del siglo V, el matemático y astrónomo chino Zu Chongzhi calculó el valor de π en 3,1415926, al que llamó «valor por defecto», y 3,1415927, «valor por exceso», y dio dos aproximaciones racionales de π, 22/7 y 355/113, muy conocidas ambas,12 siendo la última aproximación tan buena y precisa que no fue igualada hasta más de nueve siglos después, en el siglo XV.10
Matemática india[editar]
Usando un polígono regular inscrito de 384 lados, a finales del siglo V el matemático indio Aryabhata estimó el valor en 3,1416. A mediados del siglo VII, estimando incorrecta la aproximación de Aryabhata, Brahmagupta calcula π como  , cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.8
, cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.8
 , cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.8
, cálculo mucho menos preciso que el de su predecesor. Hacia 1400 Madhava obtiene una aproximación exacta hasta 11 dígitos (3,14159265359), siendo el primero en emplear series para realizar la estimación.8Matemática islámica[editar]
En el siglo IX Al-Jwarizmi, en su Álgebra (Hisab al yabr ua al muqabala), hace notar que el hombre práctico usa 22/7 como valor de π, el geómetra usa 3, y el astrónomo 3,1416. En el siglo XV, el matemático persa Ghiyath al-Kashi fue capaz de calcular el valor aproximado de π con nueve dígitos, empleando una base numérica sexagesimal, lo que equivale a una aproximación de 16 dígitos decimales: 2π = 6,2831853071795865.
Renacimiento europeo[editar]
A partir del siglo XII, con el uso de cifras arábigas en los cálculos, se facilitó mucho la posibilidad de obtener mejores cálculos para π. El matemático Fibonacci (1170-1250), en su Practica Geometriae, amplifica el método de Arquímedes, proporcionando un intervalo más estrecho. Algunos matemáticos del siglo XVII, como Viète, usaron polígonos de hasta 393.216 lados para aproximarse con buena precisión a 3,141592653. En 1593 el flamenco Adriaan van Roomen (Adrianus Romanus) obtiene una precisión de 16 dígitos decimales usando el método de Arquímedes.
Época moderna (precomputacional)[editar]
En 1610 el matemático Ludolph van Ceulen calculó los 35 primeros decimales de π. Se dice que estaba tan orgulloso de esta hazaña que lo mandó grabar en su lápida. Los libros de matemática alemanes durante muchos años denominaron a π como número ludolfiano. En 1665 Isaac Newton desarrolla la serie13
Con  obtuvo una serie para:
obtuvo una serie para:
 obtuvo una serie para:
obtuvo una serie para:
En 1699, a sugerencia de Edmond Halley, el matemático inglés Abraham Sharp (1651-1742) calculó pi con una precisión de 71 dígitos decimales usando la serie de Gregory:
Con  se obtiene una serie para:
se obtiene una serie para:
 se obtiene una serie para:
se obtiene una serie para:
Para alcanzar la precisión obtenida, debió usar alrededor de trescientos términos en la serie. En 1720 el francés Thomas de Lagny utilizó el mismo método para obtener una aproximación de 127 dígitos (solo los primeros 112 eran correctos).
Leibniz calculó de una forma más complicada en 1682 la siguiente serie matemática que lleva su nombre:
 .
.
El inglés William Oughtred fue el primero que empleó la letra griega π como símbolo del cociente entre las longitudes de una circunferencia y su diámetro. Fue en el año 1706cuando el galés William Jones afirmó: «3,14159 andc. = π» y propuso usar siempre el símbolo π, y fue Leonhard Euler el que al adoptarlo en 1737 lo convirtió en la notación habitual que se usa hasta nuestros días.
El matemático japonés Takebe empezó a calcular el número π en el año 1722, con el mismo método expuesto por Arquímedes, y fue ampliando el número de lados para polígonos circunscritos e inscritos hasta llegar a 1.024 lados. Este ingente trabajo consiguió que se determinara π con 41 decimales.
En 1789 el matemático de origen esloveno Jurij Vega, mediante la fórmula de John Machin, descubierta en 1706, fue el primero en averiguar los primeros 140 decimales de π, de los cuales 126 eran correctos; este récord se mantuvo durante 52 años, hasta que en 1841 William Rutherford calculó 208 decimales, de los cuales 152 eran correctos.
El matemático aficionado de origen inglés William Shanks trabajó, durante 20 años, en hallar los guarismos de π, habiendo obtenido 707 decimales en 1873. En el año 1944, D. F. Ferguson encontró un error en en el quingentésimo vigésimo octavo guarismo decimal (528º) de la serie de Shanks, a partir del cual todos los dígitos subsiguientes eran erróneos.14 En 1947, Ferguson recalculó π con 808 decimales con la ayuda de una calculadora mecánica.[cita requerida]
Algunas aproximaciones históricas de valores de π, anteriores a la época computacional, se muestran en la siguiente tabla:
| Año | Matemático o documento | Cultura | Aproximación | Error
(en partes por millón)
|
| ~1900 a. C. | Papiro de Ahmes | Egipcia | 28/34 ~ 3,1605 | 6016 ppm |
| ~1600 a. C. | Tablilla de Susa | Babilónica | 25/8 = 3,125 | 5282 ppm |
| ~600 a. C. | La Biblia (Reyes I, 7,23) | Judía | 3 | 45 070 ppm |
| ~500 a. C. | Bandhayana | India | 3,09 | 16 422 ppm |
| ~250 a. C. | Arquímedes de Siracusa | Griega | entre 3 10/71 y 3 1/7
empleó 211875/67441 ~ 3,14163
| <402 br="" ppm="">
13,45 ppm
|
| ~150 | Claudio Ptolomeo | Greco-egipcia | 377/120 = 3,141666... | 23,56 ppm |
| 263 | Liu Hui | China | 3,14159 | 0,84 ppm |
| 263 | Wang Fan | China | 157/50 = 3,14 | 507 ppm |
| ~300 | Chang Hong | China | 101/2 ~ 3,1623 | 6584 ppm |
| ~500 | Zu Chongzhi | China | entre 3,1415926 y 3,1415929 empleó 355/113 ~ 3,1415929 | <0 br="" ppm="">0,085 ppm |
| ~500 | Aryabhata | India | 3,1416 | 2,34 ppm |
| ~600 | Brahmagupta | India | 101/2 ~ 3,1623 | 6584 ppm |
| ~800 | Al-Juarismi | Persa | 3,1416 | 2,34 ppm |
| 1220 | Fibonacci | Italiana | 3,141818 | 72,73 ppm |
| 1400 | Madhava | India | 3,14159265359 | 0,085 ppm |
| 1424 | Al-Kashi | Persa | 2π = 6,2831853071795865 | 0,1 ppm |
SIGA LA LECTURA DE ESTA APASIONANTE HISTORIA AQUÍ:
http://es.wikipedia.org/wiki/N%C3%BAmero_%CF%80
EDICIÓN, TRANSCRIPCIÓN: LICENCIADO EN HISTORIA VICTOR MANUEL GRUBER DE FIGARELLI, UCV CARACAS, VENEZUELA, 1976








.png/220px-Egyptian_A'h-mos%C3%A8_or_Rhind_Papyrus_(1065x1330).png)


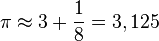


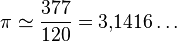




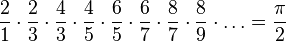



1 comentario:
Hace 60 años (1955) mi hermano gemelo Antonio (+) y yo, descubrimos cómo calcular el no. PI, gracias a un gran Maestro y
Geometra, Profesor Pedro Hernandez, de grata memoria. Liceo Andrés Bello, 5o. Año de de Física y Matemáticas, Carcas, Venezuela.
¡Dios los tenga en su Gloria Eterna: Amén!
Publicar un comentario